Image DOTS

Enregistrement de données et algorithmes récursifs

Ce tutoriel est inspiré du site web Koalas To The Max dont le but évident est de stimuler l'oisiveté de l'internaute en lui faisant apparaître progressivement une image de Koala.

L'image de base est un gros point qui se subdivise en quatre plus petits points à chaque passage de souris jusqu'à l'apparition de plus en plus claire de l'image :

Sans nier l'efficacité de ce site à remplir son objectif (vous faire perdre votre temps), je vous propose d'en perdre un peu plus en reproduisant ce procédé avec Grasshopper sur une image du logo de Rhino (pour des questions de performances d'affichage). Cela nous permettra d'aborder les questions d'enregistrement des données et des algorithmes récursifs (avec des itérations). On utilise pour ce dernier point le plug-in HoopSnake.

PARTIE 1 - GRILLE DE BASE ET AFFICHAGE DES POINTS

HoopSnake est un plug-in qui permet d'effectuer plusieurs itérations d'un même algorithme. Ainsi, à partir d'une grille qu'on subdivise au passage de la souris, on obtiendra une nouvelle grille plus fine qui remplacera l'ancienne comme donnée d'entrée de l'algorithme de subdivision.

Dans Grasshopper, voici les étapes permettent d'établir la grille de base et d'afficher les premiers points de couleurs.

• Création de la grille de base :
  • On crée une grille de rectangles avec Square (grid), celle-ci devant contenir initialement 4 points, on rentre un Panel avec le nombre 2 pour les input Extend X et Extend Y (nombre des divisions en X et en Y).
  • Pour déterminer la taille des cellules (input Size), on utilise Division pour diviser la taille de l'image (ici un Panel contenant 2248, nombre de pixels dans chaque direction du logo) que l'on divise par nombre de divisions (2).
  • Cette grille sert de donnée de base à HoopSnake (input Starting Data).

• Affichage des points de couleur :
  • A ce stade, la donnée de sortie de HoopSnake (output Feedback) est toujours la grille initiale. On la relie à un composant Polygon Center afin de trouver les points au centre de chacune des cellules.
  • Avec Curve Closest Point, on trouve le point le plus proche de ce centre (input Point) sur la cellule (input Curve). 
  • On trace un cercle (composant Circle) de centre (input Plane) le point central du Polygone et de rayon la distance du centre au bord de la cellule (output Distance de Curve Closest Point). Avec Surface on transforme le cercle en disque.
  • On insère l'image du logo de Rhino dans un Image Sampler en redéfinissant bien les domaines X et Y à la taille de l'image (de 0 à 2248). On précise le Channel (donnée de sortie de l'Image Sampler) en demandant la couleur (RGVB Colours). Il reste à rentrer le point du centre de la cellule en input à l'Image Sampler pour obtenir en output la couleur correspondant à ce point.
  • Enfin avec Custum Preview, on demande à Rhino de montrer le disque (input Geometry) avec sa couleur (input Shader).

Ci-dessous le logigramme de la grille initiale et son affichage en points de couleurs :

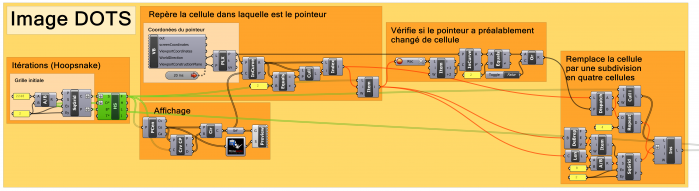
PARTIE 2 - CRÉATION DE LA NOUVELLE GRILLE APRES ITÉRATION

 Cette partie se divise en trois blocs interconnectés :

• Un premier permet de savoir dans quelle cellule se situe le pointeur de la souris
• Le second vérifie si le pointeur a préalablement changé de cellule. En effet, si le pointeur reste dans le même cercle, il faut que celui ne se subdivise qu(une seule fois. Dans le cas contraire, un cercle se subdiviserait à l'infini tel une fractale.
• Le dernier bloc remplace la cellule où se situe le pointeur par 4 cellules de dimensions deux fois inférieures.

Dans Grasshopper, voici les étapes permettent d'établir la nouvelle grille itérée.

• Bloc 1 - Repérage de la cellule dans laquelle se trouve le pointeur :
  • Pour trouver les coordonnées XY du pointeur, j'ai utilisé un code VB trouvé sur le forum de Grasshopper et écrit par Richard Schaffranek. Etant donné que ce n'est pas l'objet du tutoriel, je le donne ci-dessous sans l'expliquer :
    

    Dim Point1 As  System.Drawing.Point = System.Windows.Forms.Cursor.Position
    Dim point2 As  System.Drawing.Point
    point2 = doc.Views.ActiveView.ScreenToClient(Point1)
    screenCoordinates = point1 ' doc.Views.ActiveView.ActiveViewport.ClientToWorld(point2)
    ViewportCoordinates = Point2
    WorldDirection = doc.Views.ActiveView.ActiveViewport.ClientToWorld(point2)
    ViewportConstructionPlane = doc.Views.ActiveView.ActiveViewport.ConstructionPlane()

  • Ce VB Script est relié à un Timer réglé à 20 ms afin de mettre à jour les coordonnées du pointeur très régulièrement.
  • Line/Plane entre les outputs WorldDirection (input Line) et ViewConstructionPlane (input Plane) permet d'obtenir le point du plan sous le curseur de la souris dans l'output Point.
  • Grâce à Point In Curve, on peut tester si le point du curseur (input Point) se situe dans les cercles (input Curves). L'output Relationship retournera pour chaque cellule 0 si le curseur ne se situe pas dans son cercle inscrit et 2 si, au contraire, il s'y trouve.
  • Avec Equal on teste si chacune des Relationship (input A) est égale ou non à 2 (input B).
  • En insérant l'output Equality dans un Cull Pattern, on ne garde des Relationship (input List) que celui qui est égal à 2 (s'il existe, il se peut que le pointeur soit dans une cellule mais pas dans le cercle inscrit, il n'y a alors aucun résultat positif).
  • Avec Item Index (Relationship en input List et l'output List du Cull Pattern en input Item), on obtient l'index de la cellule contenant le cercle où se situe le pointeur. 
  • Avec List Item sur les cellules en sortie de Hoopsnake (input List) on ne retient que la cellule correspondant à l'index trouvé (input Index).

• Bloc 2 - Vérifier si le pointeur a préalablement changé de cellule :
  
  • On enregistre les trois dernières cellules où a été le curseur avec un Data Recorder (Record Limit = 3). En effet, le dernier enregistrement correspond à la cellule se situe le curseur, celui d'avant à la transition et donc l’antépénultième correspond à la cellule où se trouvait le curseur avant un éventuel changement.
  • Grâce à un List Index (output i+2 avec i = 0), on récupère donc cette précédente cellule.
  • Avec Point In Curve, on teste si le point du curseur (input Point) se situe encore dans cette cellule (input Curves).
  • Avec Equal on teste si l'output Relationship (input A) est égale ou non à 2 (input B).
  • On insère le résultat dans l'input A d'un Gate Or, l'input B étant un Boolean Toggle bloqué sur False (cela permet d'avoir un booléen en sortie même si les trois derniers enregistrements ne contiennent aucune cellule à tester). Ainsi, si le résultat est True, il ne faut pas ré-exécuter de subdivision ; s'il est False, on peut au contraire subdiviser la cellule puisque cela prouve que le curseur provient originellement d'une autre cellule.
• Bloc 3 - Remplacement de la cellule par une subdivision en quatre cellules :
  
  • Grâce à Insert Items, on va pouvoir remplacer la cellule à subdiviser par ses quatre subdivisions.
  • En input List, on rentre donc la grille en sortie Feedback de HoopSnake à laquelle on aura préalablement ôté la cellule où se situe le curseur avec un Cull Index. En input Indices, on rentre l'output B d'un Dispatch avec en input List l'Index de la cellule et en input Dispatch pattern le résultat du Gate Or. Cette opération permet de ne pas retirer de cellule si le pointeur n'en a pas changé préalablement.
  • Ce même Index (en sortie de l'output B du Dispatch) est ainsi répété 4 fois avec Repeat Data et inséré dans l'input Indices du Insert Items.
  • On récupère avec Length la longueur du périmètre de la cellule à subdiviser. Avec Division par 8 (4 pour obtenir un côté et 2 pour sa moitié) on obtient donc la longueur du côté d'une subdivision. Cela sera la valeur d'entrée de Size d'un nouveau Square (grid). Pour les inputs Extend X et Extend Y, on prend la valeur de 2 puisqu'on veut créer 4 cellules.
  • Il reste à définir le point initial de l'input Plan de Square : pour cela on décompose la cellule initiale avec Deconstruct Brep et on sélectionne le point d'index 0 avec un List Item.
  • Le Square sera la donnée d'entrée (en mode Flatten) de l'input Item du Insert Item.
  • Enfin la nouvelle liste obtenue, qui contient la nouvelle grille, est insérée en mode Flatten dans l'input Data de HoopSnake afin de lui définir l'algorithme à itérer. Il ne reste qu'à cocher dans Hoopsnake "Monitor T* Input" et à l'activer avec Auto Loop All.
    
    

Ci-dessous le logigramme du projet et le résultats après plusieurs itérations :